Jeśli kupujemy zgrzewkę napojów, cenę możemy policzyć jako iloczyn ceny pojedynczej butelki oraz liczby butelek. I na takich przykładach uczymy się liczb i na liczbach tych działania – mnożenia. Pomijamy tu fakt, że zapominamy chociażby o jednostkach. Na tym poziomie jeśli coś daje wyrazić się liczbą – to jest liczbą. Liczba butelek, liczba złotych, liczba złotych za butelkę, nadają liczbom znaczenie. W końcu nie da się pomorzyć krów przez połać trawy. Sensowną liczbę uzyskamy gdy je podzielić, a wynik będzie miał domyślną jednostkę dość dziwnej gęstości.

Jednak o jednostkach uczymy się dopiero na fizyce, a więc po dwóch trzyletnich¹ turach nauczania. Mnożenie poznajemy wcześniej i działanie to poznajemy właśnie jako działanie na liczbach. Działanie określane jako wielokrotne dodawanie, przynajmniej dopóki trzymamy się liczb naturalnych – a od takich właśnie zaczynami poznawanie algebry. Na tym etapie poznajemy bardzo ważną cechę mnożenia – rozdzielność względem dodawania – Jednak mnożenie nie musi określać operacji wielokrotnego dodawania. Jeśli pomnożymy krowę przez 4,5, możemy dostać 4,5 krowy tylko rozpatrując ją z punktu widzenia masarza, ale na pewno nie z punktu widzenia kogoś kto ma je wydoić. Ale zostawmy na chwile w spokoju jednostki. Patrząc z punktu widzenia matematyka, jak mamy działanie – to potrzebne jest nam działanie odwrotne, a to na liczbach daje się zrobić wprowadzając liczby wymierne.

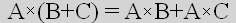
Potem w szkole poznajemy kolejne iloczyny, które wyglądają na tyle dziwnie, że nadaje się im przymiotniki. Oczywiście musimy opuścić świat liczb i wrócić do absolutnych podstaw matematyki – czyli rachunku zbiorów. To tu czai się drugi poznawany iloczyn – iloczyn kartezjański. Twór który zrozumiałem dopiero na studiach, bo wydawał mi się zupełnie dziwaczny a pokazywany na rysunkach wyglądał co najmniej podejrzanie, bo nikt nawet nie wspomniał, że narysowane są jeszcze dwa izomorfizmy. Cóż, alternatywą było założenie że 10-cio latek zauważy w płaskim rysunku mapę dwuwymiarowego ciągłego zbioru zanurzonego w co najmniej czterowymiarowej przestrzeni w której wybrane (i oznaczone) punkty są tożsame a iloczyn kartezjański jest zbiorem zbiorów dwuelementowych takich par, a właściwie cięciem w przestrzeni wysokich takich zbiorów. To oczywiste, prawda?

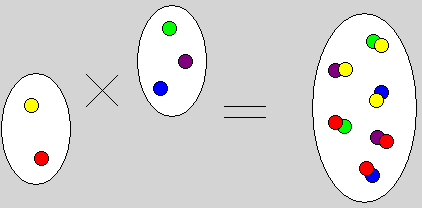
Ale iloczyn ten łatwo można zobaczyć w menu baru z chińszczyzną, w którym możemy bez problemu znaleźć ponad 80 potraw, wygenerowanych przez zmieszanie wybranego produktu wysokobiałkowego (kurczak, ryba, wieprzowina, wołowina, krewetki, kaczka, tofu a czasem i szarańcza) z wybranym zestawem przyprawowo/warzywnym (tu mamy co najmniej „curry”, „na słodko”, „pięć smaków”, „z grzybami mun” i coś na co jeszcze wpadł szef kuchni sprzątając lodówkę). Na poziomie abstrakcji zbiorów, wynik działania, znanego z tego że wynikiem mnożenia dwóch liczb – jest także liczba, nawet jeśli ukraszony przymiotnikiem – nie powinien wprowadzać nowego bytu sięgając do innej przestrzeni, a właściwie do metaprzestrzeni: zbioru zbiorów.

Łatwiej idzie z iloczynem skalarnym i wektorowym, choć raczej poddajemy się i nie próbujemy rozumieć, patrząc na wektory jako strzałki albo ciągi współrzędnych z dziwnymi regułami dodawania i mnożenia. Tymczasem właśnie w świecie wektorów interpretacja mnożenia niesie znacznie bardziej interesujące skutki. Niestety musimy wrócić do czegoś w rodzaju jednostek i wprowadzić (lub przypomnieć) jedno bardzo ważne pojęcie: izomorfizm.

Izomorfizm dwóch zbiorów – to takie odwzorowanie w którym każdemu punktów z jednego zbioru odpowiada dokładnie jeden punkt z drugiego. jeśli to jest dla nas zbyt trudne, to dobrym przykładem izomorfizmy jest znany nam izomorfizm zbiorem uczniów danej klasy a zbiorem nazwisk w dzienniku. To są dwa różne zbiory. Ich elementy mają zupełnie różne cechy (uczeń nie ma kroju pisma ani koloru linii, a nazwiska w dzienniku nie trzeba karmić), ale odpowiedniość 1:1 jest tu oczywista. To co musimy zauważyć, to że to właśnie ta oczywistość jest izomorfizmem dwóch różnych zbiorów.

Druga sprawa – to jednostki a w zasadzie różne rodzaje bytów matematycznych, czy elementy różnych zbiorów. Przykładem takich dwóch różnych bytów są wektory i skalary. Także wektory o różnej liczbie wymiarów – są elementami zupełnie rozłącznych zbiorów. Co prawda przyjęło się myśleć o wektorach 2D jako o podzbiorze wektorów 3D. Podzbiorze tworzącym płaszczyznę, ale to tylko kolejny oczywisty izomorfizm. Co ciekawe – przestrzenie wektorowe tworzą szereg który można ponumerować liczbami naturalnymi określającymi wymiar, ze skalarem jako wektorem o wymiarze zero. Niestety w przestrzeniach wektorach nie mamy mnożenia jako naturalnego działania. Co prawda mamy iloczyn skalarny, ale jego wynikiem jest skalar – a więc coś z zupełnie innej przestrzeni. Na dodatek nie daje się zdefiniować operacji odwrotnej, ze względu na niejednoznaczność. Mamy też iloczyn wektorowy, ale jest on dobrze zdefiniowany tylko w przestrzeni trójwymiarowej. Czyżby trzy wymiary maiły jakąś szczególną właściwość która sprawia, że to właśnie w naszej codziennej geometrii może istnieć coś takiego jak iloczyn wektorowy? Czy trzy wymiary mają w sobie coś boskiego?

Ponadto iloczyn wektorowy zachowuje się dość dziwnie. Nie mówię tu o tym, że jest antyprzemienny – po zamianie czynników miejscami – wynik zmienia znak. To nie jest specjalnie nietypowe. Problemem jest to, jak zachowują się przy transformacjach przestrzeni. Na przykład przy odbiciu zwierciadlanym całej przestrzeni - zmieniają znak. Dlatego wielkości takie nazywamy czasami pseudowektorami.

Zobaczmy jak zdefiniowany jest iloczyn wektorowy. Jednak zamiast rozpisywać go dokładnie współrzędna po współrzędnej, popatrzmy na wzór na którym łatwo zauważymy regułę:

Wzór wygląda prosto tylko dlatego, że zastosowaliśmy pewną konwencje która pozwala uprościć zapis. Po pierwsze, jeśli jakieś indeksy się powtarzają – oznacza to sumowanie po wszystkich możliwych wartościach tych indeksów. To częsta konwencja gdy indeksów jest dużo i zapisywanie wszystkich sum symbolami ‘Σ’ tylko zaciemniałoby obraz tego co jest sumowane. Po drugie wprowadziliśmy symbol ‘ε’ który oznacza w zależności od tego czy indeksy się powtarzają – 0, jeśli są w dobrej kolejności, albo zamienione parzystą liczbę razy – wartością jest 1. Jeśli nieparzystą liczbę razy zamieniliśmy kolejność indeksów - -1.

Gdybyśmy chcieli określić iloczyn w przestrzeni dwuwymiarowej – to zabraknie nam indeksów na wektory kierunkowe. Przy czterech, musielibyśmy pomnożyć aż trzy wektory, by w wyniku uzyskać wektor. A jeśli chcemy mnożyć dwa? Co dostaniemy. No cóż. Dostaniemy coś co pomnożone przez wektor – da w wyniku wektor, ale coś co niesie informację o kierunkach wcześniej pomnożonych wektorów. Coś co ma aż sześć współrzędnych!.

Matematycy taki twór nazywają dwuwektorem. To jakby zorientowana w przestrzeni powierzchnia. Która nie ma kształtu, a jedynie wartość i orientację, podobnie jak wektor – ma wartość i kierunek (zwrot jest dla mnie elementem kierunku). Może więc iloczyn wektorowy wcale nie daje w wyniku wektora – ale właśnie duwektor także w przestrzeniach o innej liczbie wymiarów. Tylko że dwuwektor ma w przestrzeniach o różnej liczbie wymiarów - rożne liczby współrzędnych. Na płaszczyźnie dwuwymiarowej trudno musi mieć taki kierunek jak płaszczyzna, choć może mieć ujemny znak. Dlatego mnożąc dwa wektory w przestrzeni dwuwymiarowej – dostajemy tylko liczbę. W przestrzeni trójwymiarowej – w wyniku otrzymamy twór który ma trzy współrzędne – podobnie jak wektor, dlatego z wektorem można go pomylić. Mówimy że istnieje naturalny izomorfizm między przestrzenią wektorów i przestrzenią dwuwektorów zanurzonych w przestrzeni trójwymiarowej – kierunek wektora odpowiada kierunkowi normalnej do kierunku płaszczyzny dwuwektora, a wartość to wartość. Dwuwektory tworzą także przestrzeń wektorową. Można je dodawać i mnożyć przez skalar. Czy można więcej? Oczywiście! Dwuwektor pomnożony przez wektor – daje trójwektor, tylko że w przestrzeni trójwymiarowej – trójwektor nie ma już swobody wyboru kierunku. Tu mamy izomorfizm ze skalarem – choć geometrycznie – mówimy o objętości, tylko że objętości skierowanej (może mieć dwa zwroty – do wewnątrz i na zewnątrz). W przestrzeni czterowymiarowej – trójwektor jest izomorficzny z wektorem.

Zauważmy, że dodanie mnożenia do zbioru wszystkich wektorów wprowadza nam nowy typ bytów geometrycznych jeszcze zanim spróbowaliśmy dołożyć działanie odwrotne, a to wymaga wprowadzenia ujemnej krotności wektora! Czy możemy sobie wyobrazić minusjednowektor²? I czym miałby taki twór się charakteryzować? Zacznijmy od najprostszej cechy – pomnożony przez wektor powinien dawać skalar. Coś takiego robi to iloczyn skalarny, który wymaga podania kierunku i jednostki (w postaci drugiego wektora). Jednostki w której „mierzymy” wektory. A czy można dwuwektor zredukować do wektora? Gdybyśmy go zmierzyli w wybranym kierunku – dostaniemy wartość w kierunku prostopadłym, a to zaczyna pachnieć doświadczeniami z polaryzacją w mechanice kwantowej. Możemy także mierzyć trójwektory minusdwuwektorami otrzymując wektor, a iloczyn który tu przedstawiliśmy nosi nazwę iloczynu Grasmana.

Ale czy to wszystko ma jakiś sens który wykracza poza czysta matematykę? Cóż… Jeśli tylko popatrzymy na zastosowania wyższej matematyki – to iloczyn Grasmana pojawia się w każdym wzorze zawierającym całki w których symbol dx – to nic innego jak określenie miary – a to co jest pod całką – jest jednowektorem – tylko że w przestrzeni jednowymiarowej i dopiero przy całkach podwójnych i potrójnych możemy w nich dostrzec wielowektory.