W szkole poznajemy zestaw prostych narzędzi które pozwalają na policzenie wszystkiego co potrzebujemy z elektryczności i dość sporo z elektroniki. Co prawda w codziennym życiu nie mamy zbyt wielu okazji by tą wiedzę wykorzystać, ale czasami bywa bardzo przydatna by zrozumieć dlaczego kosiarka podłączona do długiego cienkiego przedłużacza ma mniejszą moc, i dlaczego nie da się uruchomić samochodu jeśli nie dokręcimy akumulatora.

Pomimo pozornie niewielkiej użyteczności tej wiedzy, na lekcjach fizyki zdarza się liczyć zadania które zajmują sporo czasu i które w zasadzie niczego nie wnoszą. Popatrzmy na jedno takie zadanie:

Proszę policzyć oporność zastępczą obwodu widzianego ze strony baterii, prąd płynący przez opornik R3 oraz napięcie na oporniku R4.¹

Zadanie to wygląda na sposób pozwalający nauczycielowi na dość sporo luzu. Liczenie tego na pewno zajmie całą lekcję a resztę można zadać do domu. Ale weźmy się za rozwiązywanie. Do dyspozycji mamy prawo Ohma, oraz dwa prawa Kirchoffa:

Prąd płynący przez przewodnik jest proporcjonalny do przyłożonego do tego przewodnika napięcia. Współczynnik proporcjonalności nazywamy przewodnością, a jej odwrotność - oporem.

Suma prądów wpływających do dowolnego punktu obwodu jest równa sumie prądów z niego wypływających.

Suma napięć liczonych po drodze zamkniętej w obwodzie jest równa 0.

Do policzenia mamy tylko jeden prąd i jedno napięcie oraz opór zastępczy, ale żeby się z tym uporać musimy policzyć pewien układ równań. Możemy te równania ułożyć korzystając z podanych wyżej zależności, ale niestety konieczne będzie zbudowanie układu równań zawierającego wszystkie natężenia i prądy – czyli aż 14 zmiennych. To oznacza, że potrzebujemy aż 14 równań! Co prawda bez problemu je wyznaczymy, ale rozwiązywanie trochę czasu może nam zająć.

Możemy też przyjrzeć się uważnie rysunkowi, by zauważyć, że oporniki są tylko narysowane tak wrednie, bo tak naprawdę jest to wielokrotnie stosowane połączenie szeregowo-równoległe

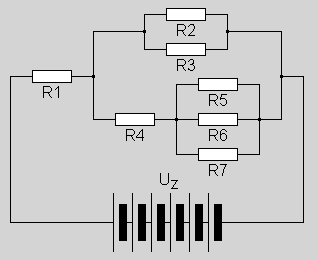
Teraz pomocne będą wymienione wcześniej prawa. Pierwsze prawo Kirchoffa w szczególnym przypadku sprowadza się do tego że w każdym punkcie obwodu szeregowego prąd jest taki sam. Podobnie drugie prawo stosuje się do połączenia równoległego i prowadzi do wniosku, że na każdym równolegle podłączonym odbiorniku – napięcie jest takie samo. Z prawa Ohma i powyższych wniosków wynika, że przy szeregowym połączeniu oporników – dodaje się opory (rezystancje), a przy równoległym – przewodności (konduktancje). Przewodność – jest odwrotnością oporu. To pozwala nam na policzenie oporności zastępczej, całego obwodu która pozwoli na policzenie całkowitego prądu. Zrezygnujemy tu jednak z próby wyprowadzenia ostatecznego wzory – bo poza ćwiczeniem małpiej umiejętności przekształcania wzorów nie zbliża nas specjalnie do wyniku. Zamiast tego posłużymy się arkuszem kalkulacyjnym, bo obliczenia co prawda się proste, ale zależą od poprzednich wyników, te od jeszcze poprzednich i tak aż do danych podstawowych – poszczególnych oporności i całkowitego napięcia. Arkusz kalkulacyjny się do tego najlepiej nadaje, ponieważ w poszczególnych komórkach możemy umieścić nie tylko liczby, ale także formuły pozwalające na obliczenie wyniku na podstawie zawartości innych komórek.

Zbudujmy nasz arkusz. W kolejnych wierszach będziemy mieli dane dla każdego z oporów, w kolumnach – odpowiednio opór, przewodność, natężenie i napięcie. Oprócz oporów które są oporami zastępczymi, także tymi które trzeba policzyć pośrednio. Cała trudność polega na takim rozpisaniu oporności, by mieć połączenie szeregowe lub równoległe z opornościami które już znamy

Zastosowaliśmy tu takie same nazwy poszczególnych zastępczych oporności – jak na arkuszu:

Na razie mamy dane. Pora na obliczenia. Na początek to co jest oczywiste – czyli odwrotności oporów. Tu nie musimy wpisywać wszystkich wartości, Wystarczy zapisać w pierwszej komórce „=1/C3” (czyli odwrotność zawartości komórki C3) następnie sk0piowac tą komórkę do schowka, zaznaczyć zakres komórek – od D4 do D9, i w nie tą wartość skopiować. Przy kopiowaniu lub przenoszeniu komórek zawierających formuły – są one przenumerowowywane.

Teraz możemy zauważyć, że da się policzyć R[=23], a właściwie jego odwrotność jako sumę odwrotności odpowiednich oporów. Opór wyznaczamy jako odwrotność odwrotności: Podobnie możemy zrobić z kolejna opornością zastępczą – tym razem dodają trzy odwrotności.

Po wyliczeniu wszystkich oporów mamy wreszcie sytuacje, gdy mamy w jednym wierszu zarówno napięcie i opór. To pozwala policzyć nam natężenie, a ponieważ ten prąd płynie w obwodzie szeregowym – możemy go skopiować do odpowiednich komórek. Niestety tu nie możemy użyć copy-paste, bo tak przydatne wcześniej przenumerowanie nam trochę zaszkodzi. Tu trzeba po prostu napisać że wartość w tej komórce ma być równa wartości w komórce wskazanej:

Mając wartości prądu, możemy policzyć napięcia, przy okazji przenosząc je wtedy gdy dotyczą obwodów połączonych równolegle:

Po wykonaniu tej operacji wielokrotnie – gdy nie mamy prądu lub napięcia – liczymy do z tej drugiej wartości i oporu. Gdy mamy zarówno prąd jak i napięcie – patrzymy które z nich i gdzie należy przenieść. Operację powtarzamy aż do całkowitego wypełnienia arkusza:

Ten sposób rozwiązywania będzie bardzo wygodny także na tablicy – nie pogubimy się, tylko niestety będziemy musieli pracować na liczbach, odpadnie nam więc mozliwość prostego podejścia także to takiego zadania które posiada także część B: Policz te wartości dla podobnego obwodu w którym wszystkie oporności są identyczne. Nawet jeśli będą wynosić „R” – to ze względu na to, że opory będą się skalować liniowo – wystarczy policzyć nasz obwód dla jednego oma, a potem Prądy podzielić przez R.