Jedną z pierwszych reguł optyki geometrycznej stworzył pochodzący z Aten Euklides. Polegała ona na tym, że kąt padania promienia świetlnego na płaską powierzchnię równa się kątowi jego odbicia. Grecki matematyk zaobserwował również, że światło rozchodzi się prostoliniowo. W obecnych czasach istnienie laserów emitujących spójne wiązki światła, charakteryzujące się niewielką rozbieżnością, ułatwia nam zrozumienie optyki geometrycznej, które swoje założenia opiera na teorii istnienia promienia świetlnego, czyli możliwie najwęższej, rozchodzącej się prostoliniowo w ośrodkach jednorodnych wiązce światła.

Wyróżnia się kilka sposobów otrzymywania wiązki laserowej, jednak to zalety i niskie koszty produkcji diod półprzewodnikowych sprawiły, że stały się one bardzo popularne i są dostępne niemal w każdym supermarkecie. Najpopularniejszymi zastosowaniami jest wykorzystywanie ich w napędach CD/DVD/Blu-ray oraz we wskaźnikach laserowych.

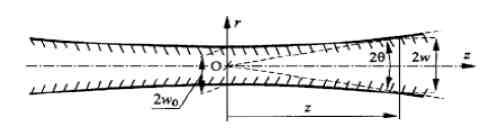
Kolejnym dogmatem optyki geometrycznej jest prawo załamania światła na granicy dwóch ośrodków, o różnej gęstości, a co za tym idzie o różnej prędkości rozchodzenia się w nich światła. Jest to uzależnione od przenikalności elektrycznej i magnetycznej ośrodka w którym propaguje się światło. Już samo powietrze, będące mieszaniną gazów spowalnia światło o około 81 [km/s] od wartości prędkości światła w próżni wynoszącej c =299 792 458 [m/s]. W transparentnych ośrodkach, które są cieczami lub też ciałami stałymi prędkość światła ulega znacznemu zmniejszeniu, sięgającemu nawet ok. 58% prędkości światła w próżni. Stosunek prędkości światła w dwóch ośrodkach oznaczamy n,

gdzie v₁ to prędkość światła w ośrodku z którego wychodzi, a v₂ to prędkość światła w ośrodku, do którego światło trafia.

Holenderski matematyk zwany Snelliusem w 1621 r. odkrył zależność pomiędzy kątem wiązki światła wpadającej do przeźroczystego ośrodka i kątem wiązki w nim załamanej. Korzystając z funkcji trygonometrycznych przedstawił ją następująco:

Nasza maszyna ma za zadanie mierzyć wysokość szklanej płytki, jej współczynnik załamania oraz prędkość propagacji światła w tym ośrodku. Podstawowe prawo mówiące o tym, że kąt odbicia równy jest kątowi padania pomoże nam ustalić wysokość badanego materiału. Na poniższej rycinie zaznaczone są stosunki przyprostokątnych trójkąta prostokątnego wraz z przykładowymi wartościami. Znając odległość lasera nad powierzchnią podłoża, odległość pomiędzy punktem przecięcia się osi lasera z osią przezroczystego elementu, na którym będą wyświetlane odbite wiązki, oraz kąt pomiędzy osią przezroczystego elementu z osią lasera jesteśmy w stanie wyliczyć wysokość szklanej płytki.

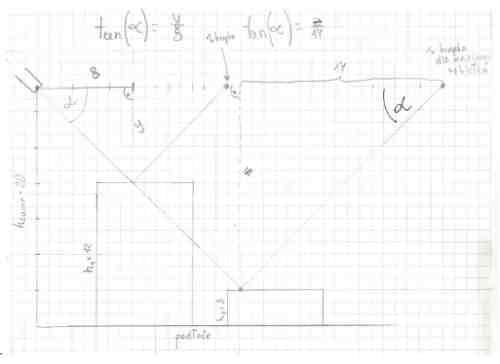
Ponieważ istnieje zależność pomiędzy kątem padania wiązki na dany materiał (α), a kątem załamania (β) możemy obliczyć współczynnik załamania względnego znając kąt ustawienia lasera względem powierzchni, a co za tym idzie sinusa z tej wartości. Z oczywistych przyczyn nie możemy bezpośrednio zmierzyć kąta ponieważ szkiełko ma pozostać niedotknięte. Sinus kąta to tak naprawdę stosunek połowy odległości odcinka pomiędzy punktem wejścia i wyjścia wiązki lasera (x) do odcinka pomiędzy punktem wewnętrznego odbicia, a punktem wejściem wiązki lasera do szkiełka (przeciwprostokątna „j”), a więc

Korzystając ze wzoru Pitagorasa

Aby poznać współczynnik załamania szklanej płytki potrzebna nam będzie wysokość obliczona wcześniej.

Do obliczeń sinusów i tangensów kąty w stopniach będziemy zamieniać na radiany za pomocą wzoru: απ/180˚, znając też wysokość na której znajduje się laser oraz kąt pomiędzy płaszczyzną równoległą do powierzchni ziemi a wiązką lasera (γ=90˚-α). Następnie musimy obliczyć wysokość trójkąta równoramiennego mającego podstawę pomiędzy laserem, a punktem przecięcia pierwszej wiązki wychodzącej ze szkiełka z linijką.

W darmowym programie symulującym zjawiska optyczne sprawdziliśmy działanie powyższych zależności.

1. Przyrządziliśmy schemat urządzenia pomiarowego

2. Skonstruowaliśmy urządzenie pomiarowe z dostępnych materiałów.

3. Przygotowaliśmy badany materiał i oczyściliśmy go z widocznych zabrudzeń.

4. Położyliśmy materiał na równej i płaskiej powierzchni.
5. Urządzenie pomiarowe ustawiliśmy równolegle z badanym materiałem, tak aby badany materiał leżał w jego centrum.
6. Odczytaliśmy kąt padania wiązki lasera (α).
7. Dostosowaliśmy położenie urządzenia tak, aby dwie wiązki wychodzące z przezroczystego materiału przechodziły przez element z podziałką.
8. W przypadku, gdy wiązki wychodziły poza element z podziałką zmniejszyliśmy kąt padania lasera i powtórzyliśmy punkt 7.
9. Odczytaliśmy w milimetrach odległość pierwszej kropki od lasera (licząc od 0 na podziałce).
10. Aby otrzymać grubość mierzonego materiału, mierzoną odległość podstawiliśmy do wzoru w miejsce „k”, np.

11. Zmierzyliśmy w milimetrach odległość pomiędzy dwoma punktami na elemencie z podziałką.

12. Aby otrzymać względny współczynnik załamania światła podstawiliśmy do wzoru zmierzoną w poprzednim punkcie odległość jako zmienną „j” oraz obliczoną wcześniej grubość materiału w miejsce „h”.

13. Aby obliczyć prędkość rozchodzenia się światła w podanym materiale podzieliliśmy prędkość rozchodzenia się światła w powietrzu przez współczynnik załamania światła.

β- kąt załamania wiązki w szklanej płytce
α- kąt padania wiązki lasera
n- współczynnik załamania
h- wysokość szklanej płytki
l- odległość między dwoma punktami
x- połowa odległości pomiędzy punktami
j- przeciwprostokątna trójkąta, którego przyprostokątne to x i h

Stosując się do instrukcji zapisanych w metodzie wykonaliśmy pomiary i obliczenia dla 3 różnych szklanych płytek i przedstawiliśmy je w poniższej tabeli. Każdy wynik uśredniony został z 3 różnych pomiarów.

Jak widać w powyższej tabeli, urządzenie nie jest w stanie wskazać precyzyjnej wysokości szklanej płytki. Możemy odczytać ją z dokładnością do kilku milimetrów, co czyni urządzenie przydatnym w większości codziennych sytuacji. Jest to spowodowane stosunkowo dużą średnicą plamki lasera, dokładnością kątomierza oraz niedokładnością konstrukcji. Ograniczeniem konstrukcyjnym jest to, że mierzony materiał nie może być dłuższy, niż odległość pomiędzy podporami urządzenia pomiarowego oraz nie może być wyższy, niż 24 [cm].

• https://chrome.google.com/webstore/detail/ray-optics-simulation/egamlemiidmmmcccadndbjjihkcfiobh
• https://pl.wikipedia.org/wiki/Pr%C4%99dko%C5%9B%C4%87_%C5%9Bwiat%C5%82a
• http://www.fizykon.org/optyka/optyka_geometryczna_prawo_zalamania_swiatla.htm
• http://www.mif.pg.gda.pl/kfamo/LM/FT/TL03-Charakterystyka%20wiazki%20laserowej%20(01-09).pdf
• http://www.mierzymy.pl/userfiles/image/semiconduktor.jpg