Pipeta miarowa to szklany przyrząd laboratoryjny służący do pobierania i odmierzania odpowiedniej miary płynów. Z jednej strony jest ona najczęściej zwężona, aby dokładniej było można odmierzać ciecze. Po zanurzeniu pipety, nabiera ona płynu do wysokości słupa cieczy, w której ją zanurzymy, zgodnie z prawami mechaniki płynów. Następnie, jeżeli zatka się górny wlot pipety, ciśnienie zewnętrzne nie pozwoli płynowi wydostać się przez cienki wlot (ilustracja 1). Dopiero po odetkaniu górnego końca możliwe staje się wyrównanie ciśnienia przez napływające do środka powietrze, dlatego, dzięki sile grawitacji, ciecz wydostaje się z pipety.

Jednak biorąc pod uwagę warunki przedstawione w doświadczeniu, sytuacja ma się nieco inaczej. Po tym, gdy nalejemy gorącej wody do pipety i obrócimy ją, zacznie ona ogrzewać znajdujące się pod spodem powietrze, które będzie chciało wydostać się do góry. W gazach zachodzi liniowa zależność pomiędzy ich temperaturą a ciśnieniem i objętością, którą opisuje równanie Clapeyrona: pV = nRT , gdzie: p – ciśnienie, V – objętość, n – liczba moli w próbce, T – temperatura, R – uniwersalna stała gazowa ( R ≈ 8,3 J/(mol·K) ). Równanie opisuje precyzyjnie jedynie stan gazu doskonałego (czyli charakteryzującego się takimi cechami: jak brak oddziaływań międzycząsteczkowych, doskonała sprężystość zderzeń cząsteczek, znikoma objętość molekuł w porównaniu z objętością całego gazu oraz nieustanne chaotyczne ruchy cząsteczek), a w przybliżeniu również innych gazów (Atkins, Jones, 2012 s. 194). W przypadku sytuacji, jaka jest przedstawiona w zadaniu, zarówno ilość moli jest stała, więc wzrost temperatury będzie bezpośrednio wypływał na wzrost ciśnienia gazu i w konsekwencji jego objętości. Zatem gdy wraz ze wzrostem temperatury będzie proporcjonalnie wzrastać jego objętość, gaz zacznie wywierać nacisk i rozpierać znajdujący się w pipecie słup wody i częściowo wypcha go na zewnątrz. Dlatego też woda zacznie wytryskiwać w formie fontanny.

Kolejnym ważnym zagadnieniem teoretycznym związanym z doświadczeniem jest mechanika przepływu cieczy, którą dokładnie opisuje równanie Bernoulliego. Precyzuje ono, że podczas przepływu cieczy, w każdym punkcie strumienia ciśnienie jest jednakowe i równe sumie ciśnienia statycznego, hydrostatycznego i dynamicznego w danym miejscu. Suma tych wielkości jest zawsze stała, czyli:

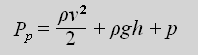
gdzie: p P - ciśnienie w dowolnym miejscu przepływu, ρ - gęstość płynu, v - prędkość płynu w rozpatrywanym miejscu, h - wysokość w układzie odniesienia, w którym liczona jest energia potencjalna, g - przyspieszenie grawitacyjne, p - ciśnienie (statyczne) płynu w rozpatrywanym miejscu. Pierwszy składnik oznacza ciśnienie dynamiczne (związane z energią kinetyczną), drugi – hydrostatyczne, a trzeci – statyczne (związane z energią potencjalną) danego płynu. Równanie to tłumaczy zjawisko zachodzące u wylotu pipety, znane też jako paradoks hydrodynamiczny. U zwężenia pipety ciśnienie statyczne przepływającej wody zmniejsza się (ponieważ w przypadku takiego przepływu nie występuje praktycznie ściśliwość cieczy. Dlatego, jako że energia przepływu musi być w każdym punkcie stała, woda w zwężeniu przyspiesza, co jeszcze wzmacnia efekt fontanny (Wikipedia, wolna encyklopedia, 2015). Potwierdziliśmy to nawet eksperymentalnie – sprawdziliśmy, czy zjawisko zajdzie dla prostej pipety szklanej, bez zwężenia na zakończeniu i nasze przypuszczenia potwierdziły się – fontanna w tym przypadku nie występowała, ponieważ słup wody nie miał wystarczającej prędkości, a zatem wystarczającej energii kinetycznej, żeby pokonać ciśnienie zewnętrzne utrzymujące go w pipecie oraz siłę grawitacji.

Aby sprawdzić doświadczalnie teorię w tym przypadku, postanowiliśmy sprawdzić efektywność zjawiska dla takich parametrów jak grubość pipety i wysokość słupa wody. Zrezygnowaliśmy ze sprawdzania zależności wysokości fontanny od temperatury wody, ponieważ, jak wynika z powyższego wstępu teoretycznego, aby zjawisko w ogóle zaszło, woda musi być bardo gorąca. Co więcej, wysokość fontanny szybko malała wraz Ilustracja 7.1. Woda utrzymująca się w pipecie po zatkaniu wlotu z ochłodzeniem wody – już po kilku minutach od zagotowania zjawisko nie zachodziło w ogóle, dlatego musieliśmy się bardo śpieszyć z eksperymentem i kontrolować za każdym razem temperaturę wody.

A. Pierwsze doświadczenie miało na celu zbadanie zależności wysokości fontanny od grubości użytej pipety

Pytanie badawcze: Jak grubość pipety miarowej wpływa na wysokość fontanny?

Hipoteza: Im większa grubość pipety, tym wyższa wytryskująca z niej fontanna.

{u Wyjaśnienie hipotezy:{ To, że fontanna wylatuje u końca pipety, związane jest z paradoksem hydrodynamicznym i tym, że w zwężeniu strumień wody, która jest wypychana przez rozgrzane powietrze, przyspiesza w zwężeniu (zjawisko opisane powyżej). Jako, że zakończenia pipet miarowych (a przynajmniej tych używanych przez nas) mają taką samą średnicę, jednak różnią się grubością, różnica między ciśnieniem statycznym będzie największa przy najgrubszej pipecie, dlatego tam woda powinna byc wystrzeliwana najwyżej.

Zmienne:

• Niezależna – grubość pipety miarowej. Manipulacja – będziemy używać pipet o różnym przekroju (mierzonym w mm).
• Zależna – wysokość fontanny (mierzona w cm, za pomocą suwmiarki).
• Kontrolowane:

Materiały:

• 4 pipety miarowe – o średnicy odpowiednio 0,2; 0,3; 0,4 i 0,6 cm
• dzban o wysokości ok. 17 cm
• kuchenka i czajnik z wodą
• suwmiarka
• miernik temperatury

Metoda:

• Zagotowujemy w czajniku odpowiednią ilość wody, by wypełnić dzban.
• Wlewamy gorącą wodę do dzbana i montujemy tam sondę do pomiaru temp.
• Wsadzamy pierwszą pipetę do dzbana na całą głębokość, pod kątem prostym. Czekamy aż wypełni się wodą.
• Zatykamy wlot pipety palcem i podstawimy pod rozsuniętą pionowo taśmę miarową (ilustracja 7.2). Obserwujemy i notujemy wysokość fontanny.
• Powtarzamy procedurę z innymi pipetami i przeprowadzamy kolejne próby.

B. Drugie doświadczenie miało na celu sprawdzić zależność wysokości fontanny od wysokości słupa wody znajdującej się w pipecie. Do doświadczenia użyto najgrubszej pipety, która okazała się dawać najwyższe wyniki w doświadczeniu A.

Pytanie badawcze: Jak wysokość słupa cieczy w pipecie wpływa na wysokość wydobywającej się z niej fontanny?

Hipoteza: Fontanna będzie najwyższa przy wypełnieniu przez wodę ok. połowy pipety.

Wyjaśnienie hipotezy: Jak wynika z analizy teoretycznej, aby woda została wyparta z pipety, powietrze znajdujące się pod nią, po obróceniu przyrządu, musi zostać podgrzane. Jeśli słup gorącej wody będzie za niski, nie da ona rady wystarczająco ogrzać takiej ilości gazu do temperatury, która pozwoliłaby, by zwiększył on swoje ciśnienie (i objętość) na tyle, aby wyprzeć ciecz z naczynia. Z kolei wraz z nadmiernym wzrostem wysokości słupa cieczy, wzrasta również jego ciężar, przez co nawet bardzo sprężone powietrze może nie dać rady wyrzucić wodę w górę. Optymalna wysokość słupa płynu powinna więc znajdować się mniej więcej w środkowej części pipety.

Zmienne:

• Niezależna – wysokość słupa wody w pipecie. Manipulacja – wysokość będziemy zmieniać wkładając pipetę na odpowiednią głębokość do dzbana z gorącą wodą (wysokości będą oznaczone na pipecie).
• Zależna – wysokość fontanny (mierzona w cm, za pomocą suwmiarki).
• Kontrolowane: temperatura wody i rodzaj użytej cieczy tak jak w tabeli 1 ORAZ:

Materiały:

• pipeta miarowa o przekroju 0,6 cm
• dzban o wysokości ok. 17 cm
• kuchenka i czajnik z wodą
• suwmiarka
• miernik temperatury
• linijka i marker

Metoda:

• Zagotowujemy w czajniku odpowiednią ilość wody, by wypełnić dzban.
• Przystawiamy do dzbana prostopadle linijkę i zaznaczamy na nim markerem od góry odpowiednie

• Wlewamy gorącą wodę do dzbana i montujemy tam sondę do pomiaru temp.
• Wsadzamy pipetę do dzbana na głębokość 2 cm (do pierwszego oznaczenia) i czekamy aż napełni się ona

• Powtarzamy procedurę za każdym razem zanurzając pipetę o „poziom” (2 cm) niżej.

A. Wyniki pierwszego doświadczenia:

Jeśli przyjrzymy się tabeli 2, to można zauważyć, że różnice w wysokościach fontann były bardzo duże w każdej próbie, ale po uśrednieniu wyników widać zdecydowaną zależność między grubością pipety a odległością, na jaką woda jest wystrzeliwana.

Dla pipety o średnicy 0,2 cm, woda w żadnej próbie nie opuściła naczynia, natomiast przy każdej następnej pipecie wysokość fontanny wzrastała wraz z grubością przekroju. Zależność proporcjonalną między obiema wielkościami potwierdza wzrastająca linia trendu. Można zatem stwierdzić, że wyniki doświadczenia potwierdziły hipotezę.

B. Wyniki drugiego doświadczenia:

Jak widać, zwłaszcza na wykresie obok – w miarę jak wzrastała wysokość słupa cieczy, rosła też wysokość fontanny. Średnio po wysokości 16 cm wielkości te były niemalże proporcjonalne. Byłoby to zgodne z hipotezą, która mówiła, że najwyższa wysokość fontanny powinna występować przy wysokości wody sięgającej do około środka wysokości pipety, jednak dalsze pomiary okazały się niemożliwe, ze względu na brak odpowiednio wysokiego naczy-nia. Zgodnie z hipotezą, dalej wysokość fontanny powinna spadać, jednak przez to, że nie mogliśmy tego sprawdzić, nie możemy do końca potwierdzić hipotezy. Wiemy natomiast że do połowy wysokości pipety wysokość fontanny rosła wraz z wysokością słupa cieczy.

Największym problemem, z jakim się spotkaliśmy podczas przeprowadzania eksperymentów był brak odpowiednio wysokiego naczynia, co uniemożliwiło potwierdzenie drugiej hipotezy. Jednak poza tym wszystkie zmienne były dokładnie kontrolowane, więc można uznać, że wyniki powinny być wiarygodne.

• Atkins P. Jones L. Chemia Ogólna wydawnictwo naukowe PWN, Warszawa, 2012
• Wikipedia, wolna encyklopedia, 2015 Paradoks hydrodynamiczny dostęp on-line: sprawdzono: 9.01.2016