Ostatnio trafiłem na artykuł w którym autor rozwodził się nad geniuszem matematyki wedyjskiej przeciwstawiając ją technikom których uczy się w szkole. Tymczasem reguły które przytoczył są przykładami „liczenia na skróty” które warto znać choćby po to by móc je od czasu do czasu zastosować zamiast sięgać po kalkulator. Szczególnie, że metody te są bardzo ciekawe i warto się przy nich na chwilę zatrzymać.
Liczenie na skróty – to sztuka coraz bardziej zapominana, ze względu na jej niewielką przydatność w świecie w którym liczby którymi operujemy mają wiele cyfr znaczących 1. Czasem taki sposób liczenia przydaje się, gdy trzeba sobie poradzić z tabliczka mnożenia, ale nauczyciele wymagają, by nauczyć się jej na pamięć. I o ile nauczenie się tabliczki mnożenia liczb jednocyfrowych – to kwestia zapamiętania 100 wyników, które można zredukować do 64 jeśli pominiemy mnożenie przez jeden (które nic nie wnosi) i przez 10 (które wymaga dopisania zera) a nawet do 40 – jeśli zaważymy, że mnożenie jest przemienne. To się jeszcze daje jakoś ogarnąć, choć i tu możemy stosować ciekawe metody liczenia na skróty.
Najprostsze jest mnożenie przez 9. Jeśli mamy pomorzyć 9 • n – to patrzymy na swoje dłonie w wyprostowanymi wszystkim palcami – poza n-tym. Liczba palców przed zgiętym palcem – to liczba dziesiątek, po – jedności.
Nieco bardziej skomplikowana procedura pozwala na mnożenie dwóch liczb większych od 5. Tu również potrzebujemy dwóch rąk – z tym, że teraz każda dłoń będzie dopowiadała jednemu czynnikowi. I każdej z rąk zginamy tyle palców o ile dany czynnik jest większy od 5. Suma wystawionych palców u obu rąk jest równa liczbie dziesiątek, a iloczyn zgiętych – liczbie jedności. Jeśli liczba jedności jest większa od 9 – to należy ją po prostu dodać do liczby dziesiątek.
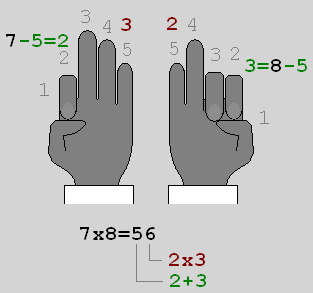
Obie te metody można łatwo wyjaśnić. W przypadku mnożenia przez 9, suma cyfr będzie zawsze równa 9 – czyli tyle ile mamy wyprostowanych palców. Liczba jedności – będzie o jeden mniejsza od liczby przez którą mnożymy – czyli dokładnie tyle palców ile znajduje się za wskazującym mnożoną liczbę. Aż dziwne że takiej prostej metody nie odkryliśmy sami w szkole w czasie sprawdzania znajomości tabliczki mnożenia. Druga metoda wymaga już trochę zachodu, ale i tu daje się wszystko wyjaśnić, choć wymyślenie tej metody wymagało pewnie trochę zabawy. Oznaczmy mnożone liczby przez x i y, a liczbę wyprostowanych i zgiętych palców odpowiednio przez w i z z dolnymi indeksami odpowiadającymi reprezentowanej liczbie.
Wtedy nasz sposób liczenia możemy zapisać jako:
- wx = x– 5
- wy = y – 5
- zx = 5- wx = 5 – (x– 5) = 5 - x + 5 = 10 - x
- zy = 10 - y
Nasz sposób liczenia na palcach możemy zapisać jako 10 * liczba dziesiątek + liczba jednostek:
- 10(wx+wy) + zxzy =
10(x-5+y-5) + (10 – x)(10 – y) =
10x + 10y – 100 + 100 – 10x – 10y + xy=
xy
Widać że wszystko się zgadza, ale jak na to wpaść?
Tabliczka mnożenia do wartości 10x10 jest dość prosta i jej zapamiętanie nie jest specjalnie skomplikowane, do bardziej złożonych obliczeń albo używamy kalkulatorów albo liczymy metodą ogólna – czyli tradycyjnie – pisemnie. Jednak taka metoda jest czasochłonna i wymaga czegoś do pisania. Tymczasem obliczenia trzeba było robić nawet wtedy gdy nie tylko nie było maszyn liczących ale i pismo nie było specjalnie popularne. Co prawda większość obliczeń nie była specjalnie skomplikowana – ale znajomość technik szybkiego, uproszczonego liczenia była w cenie. Nie musiały to być techniki super uniwersalne. Wystarczyły że działały dla liczb dwu-, góra trzy- cyfrowych.
Reguły zapisane są zazwyczaj w postaci krótkich zdań łatwych do zapamiętania. Dziś użylibyśmy wzorów, ale użycie symboli oznaczających „dowolną wartość” wynaleziono znacznie później, i jeszcze Grecy w swych rozważaniach matematycznych używali opisów słownych. Stosowane reguły nie były uniwersalne – i liczący musiał wiedzieć którą regułę zastosować w określonym miejscu, ale wynik można uzyskać na prawdę szybko. Popatrzmy na regułę mnożenia przez 11:
Mnożenie liczby dwucyfrowej przez 11 polega na wstawieniu miedzy jej cyfry – sumy tych cyfr.
Proste? Popatrzmy:
- 11*45 = 495
- 11*32 = 352
- 11*71 = 781
A jeśli wynik będzie dwucyfrowy. Cóż, wtedy pierwszą cyfrą może być tylko 1 – i tą jedynkę dodajemy do pierwszej cyfry wyniku.
Reguła wygląda na zupełnie nie matematyczną jednak zapisuje pewne spostrzeżenie:
I na koniec jeszcze jedna prosta reguła która sprawdza się gdy mnożymy dwie liczby dwucyfrowe bliskie 100. Zamiast pieczołowicie mnożyć pisemnie i dodawać, wystarczy zastosować prostą regułę – na początek odejmijmy te liczby od 100. Tak uzyskane wartości musimy tylko dodać i pomnożyć na następnie złożyć z wyników wynik mnożenia:
I znów nie ma tu nic tajemniczego; Jeśli zapiszemy nasze liczby jako różnice:
To
- xy =
(100 – a) (100 – b) =
10 000 – 100a – 100 b + ab =
100 (100-(a + b)) + ab
I znów nie ma tu żadnej magii lecz reguła która pozwala liczyć „na skróty”. Reguła przydatna – bo pozwalająca na liczenie w pamięci. I choć może się to wydawać jarmarczną sztuczką, to kiedyś było konicznością.
Literatura
- http://innemedium.pl/wiadomosc/cudowna-aryjska-matematyka